How Do You Know if the Limit Exists

A common situation where the limit of a function does not exist is when the one-sided limits exist and are not equal: the function "jumps" at the point.

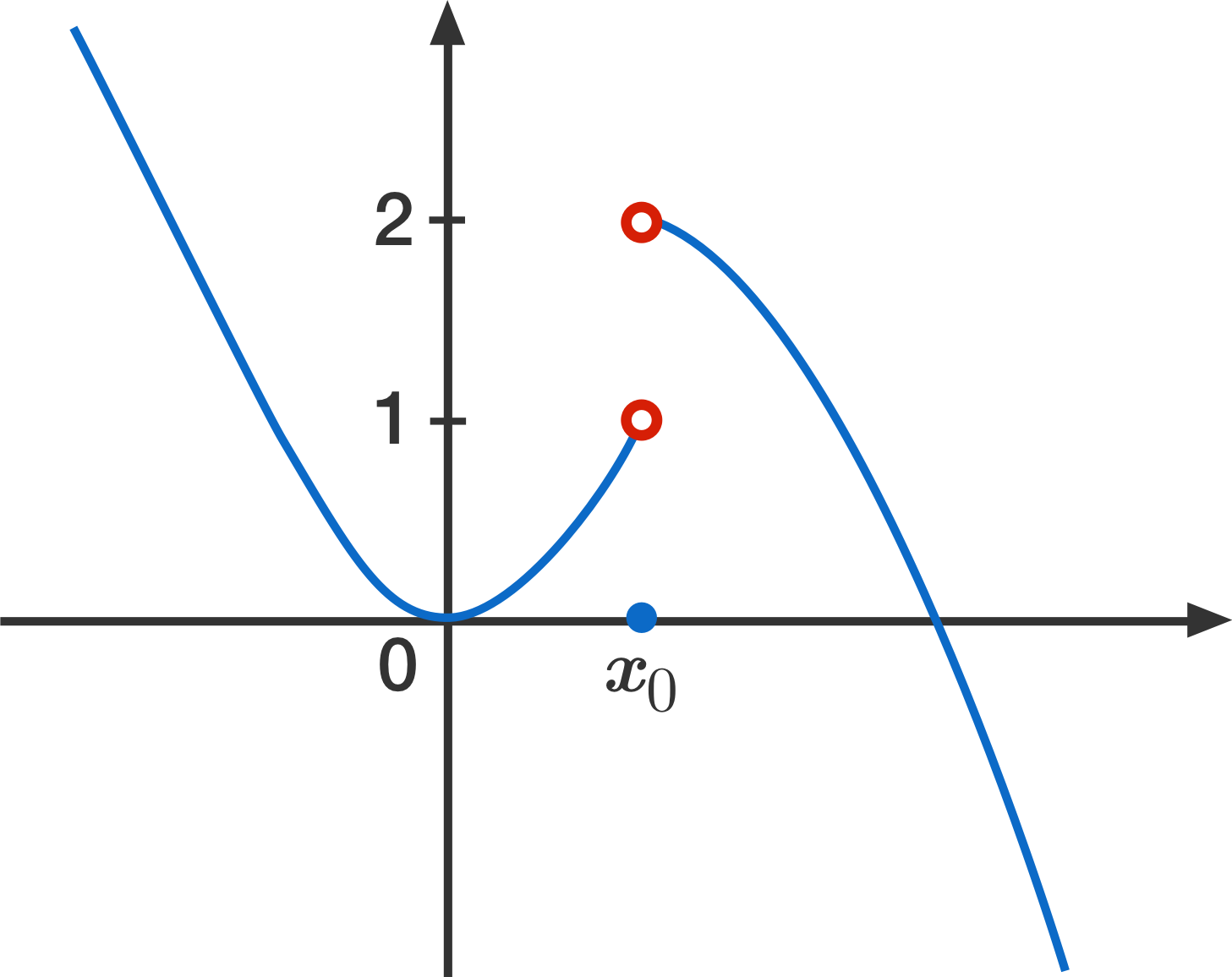The limit of $f$ at $x_0$ does not exist. ^[one]

For the role $f$ in the movie, the i-sided limits $\lim\limits_{ten\to x_0^-} f(x)$ and $\lim\limits_{x\to x_0^+} f(ten)$ both exist, simply they are not the same, which is a requirement for the (2-sided) limit to be. This is usually written

$\lim_{x \to x_0} f(x) = \text{DNE},$

where "DNE" stands for "does not exist."

Select one or more

$\lim_{x\to5^+} f(x) = 1$ $\lim_{x\to5^-} f(x) = 0$ $\lim_{x\to5^+} f(x) = iv$ $\lim_{x\to5^-} f(10) = 1$ $\lim_{10\to5^+} f(x) = 0$ $\lim_{x\to5} f(ten) \text{ does not exist}$ $\lim_{10\to5} f(10) \text{ exists}$

Let $\displaystyle f(10) = \frac{x^2-9x+twenty}{x-\lfloor x \rfloor},$ then which of the following are correct?

Notation: $\lfloor \cdot \rfloor$ denotes the flooring function.

Some other common state of affairs when limits do non be involves the part "blowing upwards" to $\infty$ or $-\infty.$ The graph is characterized by a vertical asymptote at $x=0:$

The one-sided limits of $f(x) = \frac1x$ at $x=0$ do non exist. ^[two]

While it is correct to say that $\lim\limits_{ten\to 0^-} \frac1{x}$ and $\lim\limits_{x\to 0^+} \frac1{x}$ do not exist, in this example the limits are generally written every bit

$\lim_{x\to 0^-} \frac1{x} = -\infty \qquad \text{ and }\qquad \lim_{10\to 0^+} \frac1{x} = \infty.$

This is the standard annotation that has the benefit of beingness more specific about the way in which these limits fail to exist. For the formal definitions, see the infinite limits section.

When the one-sided limits accident up in the same mode, this tin can be shortened to a unmarried two-sided limit, e.g.

$\lim_{x\to 0^-} \frac1{x^two} =\infty \qquad \text{ and }\qquad \lim_{x\to 0^+} \frac1{x^2} = \infty.$

So,

$\lim_{x\to 0} \frac1{x^2} = \infty,$

but it should exist emphasized that $\lim\limits_{ten\to 0} \frac1{x^2}$ does not exist; proverb that information technology "equals $\infty$ " is just a way of describing why it does not be.

The third course of functions which give non-existent limits are the almost exotic. If $f$ does non jump or blow up at $x_0$ but $\lim\limits_{x\to x_0} f(ten)$ does not exist, the general picture is that $f$ takes on multiple values which are far away from each other, even when its statement moves closer and closer to $x_0.$

The standard example is $f(x) = \sin \frac1x$ near $x_0 = 0.$

The function $\sin \frac1x$ oscillates infinitely often as it approaches 0. ^[iii]

If $\lim\limits_{x\to 0^+} \sin \frac1x = 50$ were truthful for some $L,$ and then the definition of limit would imply that at that place was an open interval $(0,\delta)$ such that the values of $\sin \frac1x$ for $ten$ in that interval were within, say, $0.one$ of $L.$ But no thing how small $\delta$ might be, it would have to contain $x_1 = \frac1{2N\pi}$ and $x_2 = \frac1{\large(2N+\frac12\large)\pi}$ for some sufficiently large $N.$ Since $\sin \frac1{x_1} = 0$ and $\sin \frac1{x_2} = ane,$ this is a contradiction.

All $a$ ; all $b$ Irrational $a$ ; all $b$ Irrational $a$ ; irrational $b$ No $a$ ; all $b$ No $a$ ; no $b$

$\brainstorm{aligned} f(x) &= \begin{cases} 0 &\text{ if } x \text{ is irrational} \\ 1 &\text{ if } x \text{ is rational} \end{cases} \\ grand(x) &= \begin{cases} 0 &\text{ if } ten \text{ is irrational} \\ \frac1q &\text{ if } x =\frac{p}{q}, \text{ where } p \text{ and } q \text{ are coprime nonnegative integers} \terminate{cases} \end{aligned}$

Let $f(x)$ and $g(x)$ be ii functions divers on $[0,1]$ by the formulas as described above.

For which $a \in (0,1)$ does the (deleted) $\lim\limits_{ten\to a} f(x)$ exist?

For which $b \in (0,one)$ does the (deleted) $\lim\limits_{x\to b} chiliad(x)$ exist?

Information technology is worth emphasizing that the above examples are all of functions $f$ that are defined at every point in an open interval around the indicate $x_0$ in question, except possibly for $x_0$ itself. There are other examples of functions which practice not have two-sided limits at $x_0$ considering this supposition fails.

$\lim\limits_{x\to 0} \sqrt{10}$ does not exist for the unproblematic reason that $\sqrt{ten}$ is not defined in any open interval containing $0,$ since its domain is $[0,\infty).$

$x=0$ is an endpoint of the domain for $f(x) = \sqrt{ten}.$ ^[four]

1. Alexandrov, O. Discontinuity. Retrieved September 12, 2005, from https://commons.wikimedia.org/wiki/File:Discontinuity_jump.eps.png
2. Richards, One thousand. Rectangular hyperbola. Retrieved July 2, 2008, from https://commons.wikimedia.org/wiki/File:Rectangular_hyperbola.svg
3. Thoma, M. Sin(1/x). Retrieved September 18, 2012, from https://commons.wikimedia.org/wiki/File:Sin%281x%29.svg
4. Richards, 1000. Square root. Retrieved July ii, 2008, from https://eatables.wikimedia.org/wiki/File:Square_root_0_25.svg

deatheragethessid.blogspot.com

Source: https://brilliant.org/wiki/when-does-a-limit-exist/

Share this post